[패캠 네카라쿠배 2기] 2차 테스트 - 9일차 데이터 구조7 : 트리

대표적인 데이터 구조7: 트리

1. 트리 (Tree) 구조

• 트리: Node와 Branch를 이용해서, 사이클을 이루지 않도록 구성한 데이터 구조
• 실제로 어디에 많이 사용되나?
  • 트리 중 이진 트리 (Binary Tree) 형태의 구조로, 탐색(검색) 알고리즘 구현을 위해 많이 사용됨
  • 이진 탐색 트리 O(log2N) 배열 O(n)보다 짧게 걸린다 

2. 알아둘 용어

• Node: 트리에서 데이터를 저장하는 기본 요소 (데이터와 다른 연결된 노드에 대한 Branch 정보 포함)
• Root Node: 트리 맨 위에 있는 노드
• Level: 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
• Parent Node: 어떤 노드의 다음 레벨에 연결된 노드 (해당 노드의 상단에 있는) 
• Child Node: 어떤 노드의 상위 레벨에 연결된 노드 (해당 노드의 아래)
• Leaf Node (Terminal Node): Child Node가 하나도 없는 노드
• Sibling (Brother Node): 동일한 Parent Node를 가진 노드 ex. 아래 그림의 3,6 
• Depth: 트리에서 Node가 가질 수 있는 최대 Level ex. 아래 그림은 depth가 lev2 

  

3. 이진 트리와 이진 탐색 트리 (Binary Search Tree)

• 이진 트리: 노드의 최대 Branch가 2인 트리 [트리 중 가장 많이 쓰는 트리]
• 이진 탐색 트리 (Binary Search Tree, BST): 이진 트리에 다음과 같은 추가적인 조건이 있는 트리
  • 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가지고 있음!

(출처: https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node)

4. 자료 구조 이진 탐색 트리의 장점과 주요 용도

• 주요 용도: 데이터 검색(탐색)
• 장점: 탐색 속도를 개선할 수 있음
• 이진 트리보다 이진 탐색 트리가 더 많이 사용된다

단점은 이진 탐색 트리 알고리즘 이해 후에 살펴보기로 함

이진트리와 정렬된 배열간의 탐색 비교

(출처: https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node)

 

ex. 27은 21으로 시작했을 때 14보다 28에 가깝고 25와 32중 25와 더 가깝고 25보다 크니까 내려가서 27!

각 노드들이 왼, 오 링크가 있으므로 링크드 리스트로 구현하는 것이 좋음

 

5. 파이썬 객체지향 프로그래밍으로 링크드 리스트 구현하기

5.1. 노드 클래스 만들기

In [ ]:

class Node:

def __init__(self, value):

self.value = value // 해당 값

self.left = None // 왼쪽 주소 

self.right = None // 오른쪽 주소 

 

5.2. 이진 탐색 트리에 데이터 넣기

• 이진 탐색 트리 조건에 부합하게 데이터를 넣어야 함

In [ ]:

class NodeMgmt:

def __init__(self, head):

self.head = head // root node(젤 위에 있는 노드)

def insert(self, value):

  self.current_node = self.head // 현재 노드

  while True:

    if value < self.current_node.value: // self.current_node.value = head(root node의 값이 더 크다면)

       if self.current_node.left != None: // 만약 왼쪽에 노드가 없으면

         self.current_node = self.current_node.left // 현재 노드는 현재 노드의 왼쪽(으로 보낸다)  

       else:

         self.current_node.left = Node(value) // 만약 노드가 있으면 현재 노드의 왼쪽에 새로운 노드 값을 넣는다 

         break

    else: // 만약 root node보다 크면 오른쪽으로 가야하는데 

       if self.current_node.right != None: // 오른쪽에 node가 없으면 

         self.current_node = self.current_node.right // 현재 노드를 오른쪽 노드로 

       else:

         self.current_node.right = Node(value) // 없으면 새로운 노드 생성

         break

 

In [ ]:

head = Node(1) // root node

BST = NodeMgmt(head) // root node를 가진 루트 구조를 만들었다

BST.insert(2) // 2를 가진 node를 만든다 

 

5.3. 이진 탐색 트리 탐색

In [ ]:

class NodeMgmt:

   def __init__(self, head):

     self.head = head

   def insert(self, value):

     self.current_node = self.head

while True: if value < self.current_node.value: if self.current_node.left != None: self.current_node = self.current_node.left else: self.current_node.left = Node(value) break else: if self.current_node.right != None: self.current_node = self.current_node.right else: self.current_node.right = Node(value) break

 

def search(self, value): // 원하는 값이 있는지 확인하는 

self.current_node = self.head

while self.current_node: // none이 되면 while문이 돌아가지 않는다 

if self.current_node.value == value: // 

  return True

elif value < self.current_node.value: // 값이 현재 노드보다 작으면 왼쪽으로 

self.current_node = self.current_node.left

else:

   self.current_node = self.current_node.right // 같거나 크면 오른쪽으로 

return False // 만약 일치하는 node가 없으면 while문에서 벗어나 return False

 

In [ ]:

head = Node(1)

BST = NodeMgmt(head)

BST.insert(2)

BST.insert(3)

BST.insert(0)

BST.insert(4)

BST.insert(8)

 

In [ ]:

BST.search(-1)

 

5.4. 이진 탐색 트리 삭제

• 매우 복잡함. 경우를 나누어서 이해하는 것이 좋음

5.4.1. Leaf Node 삭제 [맨 끝에 있는 node, terminal node라고도 한다]

• Leaf Node: Child Node 가 없는 Node
• parent node가 child를 가리키는 브랜치를 삭제해야 한다 
• 삭제할 Node의 Parent Node가 삭제할 Node를 가리키지 않도록 한다.
  

  

5.4.2. Child Node 가 하나인 Node 삭제

• parent node가 자신의 child node의 child node를 가리키도록 해야 한다. 
• 삭제할 Node의 Parent Node가 삭제할 Node의 Child Node를 가리키도록 한다. 

  

5.4.3. Child Node 가 두 개인 Node 삭제

1. 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키도록 한다.(삭제할 node 자리에 배치한다) 
2. // ex. 아래 그림에서 5의 오른쪽 자식 중 가장 작은 값(만약 6의 자식이 3.5, 7이 있다면 3.5)를 5의 자리에 배치 
3. // 그러면 3.5보다 작은 3이 왼쪽, 3.5보다 큰 6이 오른쪽, 6보다 큰 7이 그대로 6의 오른쪽
4. // 만약 3.5에게도 오른쪽 자식이 있으면 3.5를 올리면서 
5. 삭제할 Node의 왼쪽 자식 중, 가장 큰 값을 삭제할 Node의 Parent Node가 가리키도록 한다.(삭제할 node 자리에 배치한다) 

   

5.4.3.1. 삭제할 Node의 오른쪽 자식중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키게 할 경우

(왼쪽 그림의 6아래 왼: 3.5, 오: 7 있고, 3.5 아래 a 있다고 생각하고 시작) 

// 이렇게까지 면접에서 물어보지는 않음! 매우 어려운 부분이 맞음

• 삭제할 Node의 오른쪽 자식 선택
• 오른쪽 자식의 가장 왼쪽에 있는 Node를 선택
• 해당 Node(3.5)를 삭제할 Node의 Parent Node의 왼쪽 Branch가 가리키게 함 // ex. 6 왼쪽 3.5는 6이 5의 자리에 들어가면 6의 오른쪽에 가게 되서 안 맞기 때문에 [삭제 노드의 오른쪽의 가장 왼쪽이 삭제 노드로]
• 해당 Node(3.5)의 왼쪽 Branch가 삭제할 Node(5)의 왼쪽 Child Node를 가리키게 함 
• 해당 Node(3.5)의 오른쪽 Branch가 삭제할 Node(5)의 오른쪽 Child Node를 가리키게 함 // 위와 같은 이야기. 연결만 제대로 하라는 소리 
• 만약 해당 Node(3.5)가 오른쪽 Child Node(a)를 가지고 있었을 경우에는,
• 해당 Node의 본래 Parent Node(6)의 왼쪽 Branch(원래 3.5가 있던 자리)가 해당 오른쪽 Child Node(a)를 가리키게 함

5.5. 이진 탐색 트리 삭제 코드 구현과 분석

5.5.1 삭제할 Node 탐색

• 삭제할 Node가 없는 경우도 처리해야 함
  • 이를 위해 삭제할 Node가 없는 경우는 False를 리턴하고, 함수를 종료 시킴

# def delete(self, value): // self는 메서드 앞에 항상 쓰는 것 

searched = False // 순회하면서 찾았는지 안 찾았는지 (있으면 true로) // 순회하면서 있는지 없는지 확인

self.current_node = self.head // 순회를 해야하니까 현재 노드를 가지고 순회 시작, current_node는 삭제할 node

self.parent = self.head // 삭제를 하면 해당 노드의 parent를 가지고 작업을 해야하니까 해당 노드의 parent도 지칭하는 변수 필요 (일단 head로) // parent_node는 삭제할 current_node의 부모 

while self.current_node: // head부터 순회 

 if self.current_node.value == value: // head가 찾는 value가 맞는지, 맞으면 끝

   searched = True

   break // 찾았으니까 끝 

elif value < self.current_node.value: // 만약 내가 찾는 value가 순회하고 있는 node의 value보다 작으면 

   self.parent = self.current_node // 한칸 내려온다 

   self.current_node = self.current_node.left // 한칸 내려온다 (작으니까 left로) 

else:

  self.parent = self.current_node // 작지 않으면 (같거나 크면) 오른쪽으로 

  self.current_node = self.current_node.right

 

if searched == False: // 위의 while문이 끝난 것 : 끝난 경우의 수 1)node를 찾아서 true가 되어서 current_node에 삭제할 node, parent_node는 그 부모  2)아니면 self.current_node가 None이라 searched가 false가 되어서 내려온 것  그러므로 false인지 확인하고 false면 return 

return False

 

### 이후부터 Case들을 분리해서, 코드 작성

 

5.5.2. Case1: 삭제할 Node가 Leaf Node인 경우

In [ ]:

# self.current_node 가 삭제할 Node, self.parent는 삭제할 Node의 Parent Node인 상태

if self.current_node.left == None and self.current_node.right == None: // Leaf node인지 확인하는 

 if value < self.parent.value: // 삭제할 노드가 parent의 왼/오인지 판단  

   self.parent.left = None // 만약 value (삭제할 노드의 값)이 작으면 왼쪽이니까 noen으로 만들어서 삭제 

  else:

   self.parent.right = None // 아니면 오른쪽을 none으로 

del self.current_node // None으로 만들어서 필요 없긴하지만 더 깔끔하게 하기 위해 

 

5.5.2. Case2: 삭제할 Node가 Child Node를 한 개 가지고 있을 경우

(그림1)왼쪽인지 그림2)오른쪽인지에 따라 다름) 

In [ ]:

 

if self.current_node.left != None and self.current_node.right == None: // 왼쪽만 none이 아니다 

if value < self.parent.value: // 찾는 값이 parent 값보다 작으니까 왼쪽에 있을 것 

self.parent.left = self.current_node.left

// current_node를 삭제하니까 current_node의 왼쪽에 있는 node가 self.parent의 left로 들어간다 

else:

self.parent.right = self.current_node.left // 아니면 찾는 값이 parent값보다 크니까 오른쪽에 있을 것인데

current_node를 삭제했으니까 left로 온다  (leaf code가 left child code가 있다고 가정하고 시작)

elif self.current_node.left == None and self.current_node.right != None: // left가 아니라 right에만 있을 때 

 if value < self.parent.value: // parent보다 작으면 왼쪽에 있으니까

self.parent.left = self.current_node.right // 왼쪽에 있는 애가 current node의 자리였는데 그 자리에 삭제할 node의 오른쪽을 놓는다 ex. 위 그림에서 5의 자리에 6을 놓는다 

 else:

self.parent.right = self.current_node.right // current가 오른쪽이면 삭제하고 그자리에 current의 오른쪽을 넣는다 ex. 15자리에 17

 

// 종이에 연필과 그림을 그리고 코드를 써보고 마지막에 코드를 쳐보기 

 

5.5.3. Case3-1: 삭제할 Node가 Child Node를 두 개 가지고 있을 경우

(삭제할 Node가 Parent Node 왼쪽에 있을 때)

• 기본 사용 가능 전략
  1. 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키도록 한다.
  2. 삭제할 Node의 왼쪽 자식 중, 가장 큰 값을 삭제할 Node의 Parent Node가 가리키도록 한다.
• 기본 사용 가능 전략 중, 1번 전략을 사용하여 코드를 구현하기로 함
  • 경우의 수가 또다시 두가지가 있음
    • Case3-1-1: 삭제할 Node가 Parent Node의 왼쪽에 있고, 삭제할 Node의 오른쪽 자식 중,
    • 가장 작은 값을 가진 Node(16)의 Child Node(17)가 없을 때
    • Case3-1-2: 삭제할 Node가 Parent Node의 왼쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 오른쪽에 Child Node(17)가 있을 때 // 반드시 오른쪽만 말이 됨. 왼쪽은 더 작다는 말이라 삭제시 가장 작은 node가 위로 current_node인 15가 삭제될 때 그 자리로 올라가야 하기 때문에 
      • 가장 작은 값을 가진 Node의 Child Node가 왼쪽에 있을 경우는 없음, 왜냐하면 왼쪽 Node가 있다는 것은 해당 Node보다 더 작은 값을 가진 Node가 있다는 뜻이기 때문임

In [ ]:

if self.current_node.left != None and self.current_node.right != None: # case3 // current_node는 여기서 15

자식이 오른쪽, 왼쪽 다 있을 때 

  if value < self.parent.value: # case3-1 // 삭제할 노드(current_node(value)가 왼쪽에 있을 때 )

    self.change_node = self.current_node.right // node의 오른쪽부터 봐야(18)

    self.change_node_parent = self.current_node.right // parent의 값도 봐야 한다 16을 바꿀거면 18도 바꿔야 (18)

  while self.change_node.left != None: // 순회 시작 (!=None은 안 써도 됨) // 가장 왼쪽에 있는 값이 가장 작으니까 계속 left로 가도록 // while문으로 left가 없을 때까지 계속

   self.change_node_parent = self.change_node // 이걸 먼저하는 이유: change_node를 먼저 바꿔버리면 값이 달라지니까 지칭할 방법이 없어진다 

   self.change_node = self.change_node.left // 계속 왼쪽으로 내려가니까 위에서 parent를 해당 값으로 바꾼다

self.change_node_parent.left = None// 더 이상 왼쪽이 없을 때까지 나왔으니 해당 change_node가 가장 작으므로 본인을 삭제한다 (자신의 부모의 left(왼쪽 자식)을 none으로 만드는 것) 

if self.change_node.right != None: // right에 뭐가 있으면(17)

self.change_node_parent.left = self.change_node.right  // 본인의 부모의 left(즉 자신의 자리를) 자신의 right인 애로 바꾼다 즉 17로 

else: // right에 아무것도 없으면 

self.change_node_parent.left = None // 17이 없으면 16만 없애면 되는 것

self.parent.left = self.change_node // 15의 자리에 16을 넣어 parent인 31과 연결

self.change_node.right = self.current_node.right

// 16을 15의 자리에 넣었으니까 원래 current_node(15)의 왼, 오와 연결 

self.change_node.left = self.change_node.left

 

5.5.4. Case3-2: 삭제할 Node가 Child Node를 두 개 가지고 있을 경우

(삭제할 Node가 Parent Node 오른쪽에 있을 때)

• 기본 사용 가능 전략
  1. 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키도록 한다.
  2. 삭제할 Node의 왼쪽 자식 중, 가장 큰 값을 삭제할 Node의 Parent Node가 가리키도록 한다.
• 기본 사용 가능 전략 중, 1번 전략을 사용하여 코드를 구현하기로 함
  • 경우의 수가 또다시 두가지가 있음 : 16이 17을 1)가지는지 2)안 가지는지
    • Case3-2-1: 삭제할 Node가 Parent Node의 오른쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 Child Node가 없을 때
    • Case3-2-2: 삭제할 Node가 Parent Node의 오른쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 오른쪽에 Child Node가 있을 때
      • 가장 작은 값을 가진 Node의 Child Node가 왼쪽에 있을 경우는 없음, 왜냐하면 왼쪽 Node가 있다는 것은 해당 Node보다 더 작은 값을 가진 Node가 있다는 뜻이기 때문임

In [ ]:

 

 

삭제할 노드가 자식을 둘 다 가졌는지 

왼쪽에 있는 경우를 위에서 다뤘으니까 value<

이번에는 오른쪽에 있는 경우  value > (else로 다루는 중) 

else:

 self.change_node = self.current_node.right // 오른쪽부터 가면서 순회 시작

 self.change_node_parent = self.current_node.right // parent를 오른쪽으로 가면서 하나씩 내려가기

 while self.change_node.left != None: // 왼쪽에 아무것도 없으면 

    self.change_node_parent = self.change_node // 계속 parent는 left로 하나씩 내려간다 

    self.change_node = self.change_node.left

if self.change_node.right != None: // 위로 올라갈 가장 작은 node가 right가 없으면 

self.change_node_parent.left = self.change_node.right // 가장 작은 node의 자리 (parent의 left)에 가장 작은 node의 right값을 넣는다 

else: // 오른쪽(17) 이 없으면 

   self.change_node_parent.left = None // 18의 left 즉 자신의 자리에 아무것도 놓지 않는다  

self.parent.right = self.change_node // 실제 삭제할 node(15)의 자리 parent(10)를 위에 change_node(16)

self.change_node.left = self.current_node.left //  15의 자리에 16을 넣으면서 왼, 오 연결

self.change_node.right = self.current_node.right 

 

3-1, 3-2의 차이는 왼, 오 코드의 차이 

 

 

5.5.5. 파이썬 전체 코드 구현

In [15]:

class Node:

def __init__(self, value):

self.value = value

self.left = None

self.right = None​

 

 

class NodeMgmt:

def __init__(self, head):

self.head = head

 

def insert(self, value):

self.current_node = self.head

while True:

if value < self.current_node.value:

if self.current_node.left != None:

self.current_node = self.current_node.left

else:

self.current_node.left = Node(value)

break

else:

if self.current_node.right != None:

self.current_node = self.current_node.right

else:

self.current_node.right = Node(value)

break

 

def search(self, value):

self.current_node = self.head

while self.current_node:

if self.current_node.value == value:

return True

elif value < self.current_node.value:

self.current_node = self.current_node.left

else:

self.current_node = self.current_node.right

return False

 

def delete(self, value): # 삭제할 노드 탐색

searched = False

self.current_node = self.head

self.parent = self.head

while self.current_node:

if self.current_node.value == value:

searched = True

break

elif value < self.current_node.value:

self.parent = self.current_node

self.current_node = self.current_node.left

else:

self.parent = self.current_node

self.current_node = self.current_node.right​

if searched == False:

return False ​ # case1

if self.current_node.left == None and self.current_node.right == None:

if value < self.parent.value: self.parent.left = None else:

self.parent.right = None # case2

elif self.current_node.left != None and self.current_node.right == None:

if value < self.parent.value:

self.parent.left = self.current_node.left

else:

self.parent.right = self.current_node.left

elif self.current_node.left == None and self.current_node.right != None:

if value < self.parent.value: self.parent.left = self.current_node.right else:

self.parent.right = self.current_node.right # case 3

elif self.current_node.left != None and self.current_node.right != None: # case3-1

if value < self.parent.value:

self.change_node = self.current_node.right

self.change_node_parent = self.current_node.right

while self.change_node.left != None:

self.change_node_parent = self.change_node

self.change_node = self.change_node.left

if self.change_node.right != None:

self.change_node_parent.left = self.change_node.right

else:

self.change_node_parent.left = None

self.parent.left = self.change_node

self.change_node.right = self.current_node.right

self.change_node.left = self.change_node.left # case 3-2

else:

self.change_node = self.current_node.right

self.change_node_parent = self.current_node.right

while self.change_node.left != None:

self.change_node_parent = self.change_node

self.change_node = self.change_node.left

if self.change_node.right != None:

self.change_node_parent.left = self.change_node.right

else: self.change_node_parent.left = None

self.parent.right = self.change_node

self.change_node.right = self.current_node.right

self.change_node.left = self.current_node.left

return True

 

참고: http://ejklike.github.io/2018/01/09/traversing-a-binary-tree-1.html

Eunji Kim @ CAU - 파이썬을 사용한 이진 트리와 순회 알고리즘 구현 (1)

// 알고리즘까지 공부하고 한번 쳐보기, 비교해보기 

// 16의 17말고 17 아래 또 노드가 있어도 달라지는 것은 없다 (17을 잘 이었으니까) 

 

5.5.6. 파이썬 전체 코드 테스트

• random 라이브러리 활용
  • random.randint(첫번째 숫자, 마지막 숫자): 첫번째 숫자부터 마지막 숫자 사이에 있는 숫자를 랜덤하게 선택해서 리턴
    • 예: random.randint(0, 99): 0에서 99까지 숫자중 특정 숫자를 랜덤하게 선택해서 리턴해줌

In [19]:

# 0 ~ 999 숫자 중에서 임의로 100개를 추출해서, 이진 탐색 트리에 입력, 검색, 삭제

import random​# 0 ~ 999 중, 100 개의 숫자 랜덤 선택

bst_nums = set() // 중복을 제거하기 위해 set()사용

while len(bst_nums) != 100: 

bst_nums.add(random.randint(0, 999)) # print (bst_nums)​

# 선택된 100개의 숫자를 이진 탐색 트리에 입력, 임의로 루트노드는 500을 넣기로 함 (중간값을 넣어 균형)

head = Node(500)

binary_tree = NodeMgmt(head)

for num in bst_nums:

binary_tree.insert(num)

 

# 입력한 100개의 숫자 검색 (검색 기능 확인)

for num in bst_nums: 

if binary_tree.search(num) == False: // 문제가 있다는 뜻. 100개를 넣었기 때무에 하나라도 search가 되어야 하는데 false가 나오는 것은 트리를 잘못 구성한 것 

print ('search failed', num)​

 

# 입력한 100개의 숫자 중 10개의 숫자를 랜덤 선택

delete_nums = set() // 중복을 피하기 위해 집합으로 만든다 (random을 써서 중복될 수 있으므로) 

bst_nums = list(bst_nums) // 인덱스로 접근하기 위해 list로 

while len(delete_nums) != 10:  // 10개가 되면 멈출 것

     delete_nums.add(bst_nums[random.randint(0, 99)]) // 인덱스 번호가 0~99 

​

# 선택한 10개의 숫자를 삭제 (삭제 기능 확인)

for del_num in delete_nums:

   if binary_tree.delete(del_num) == False: // 삭제가 안 되었다는 의미 (어떤 node가 접근 불가능한 상황이 된 경우 등 )

      print('delete failed', del_num) // 어떤 숫자가 있는지를 알아보기 위해 del_num 

 

6. 이진 탐색 트리의 시간 복잡도와 단점

6.1. 시간 복잡도 (탐색시) // depth와 관련 있다. 

• depth (트리의 높이) 를 h라고 표기한다면, O(h) // depth는 위부터 0으로 시작 또는 1로 시작 // 실행 횟수 
• n개의 노드를 가진다면, ℎ=𝑙𝑜𝑔2𝑛h=log2n 에 가까우므로, 시간 복잡도는 𝑂(𝑙𝑜𝑔𝑛)
  • 참고: 빅오 표기법에서 logn 에서의 log의 밑은 10이 아니라, 2입니다.
    • 한번 실행시마다, 50%의 실행할 수도 있는 명령을 제거한다는 의미. (탐색할 후보가 줄어든다)
    • 즉 50%의 실행시간을 단축시킬 수 있다는 것을 의미함
    • 배열로 찾으면 O(n)

      

(출처: https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node)

Type Markdown and LaTeX: 𝛼2α2

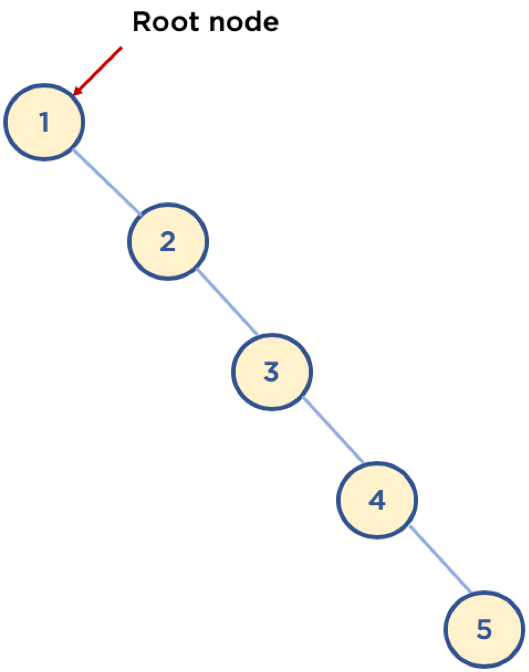
6.2. 이진 탐색 트리 단점

• 평균 시간 복잡도는 O(logn) 이지만,
  • 이는 트리가 균형잡혀 있을 때의 평균 시간복잡도이며,
• 다음 예와 같이 구성되어 있을 경우, 최악의 경우는 링크드 리스트등과 동일한 성능을 보여줌 ( O(n) )